协同算法OT算法¶

统计信息：字数 17981 阅读36分钟

协同编辑需要考虑下面几个问题：

1、怎样协同，在哪里协同（本地还是服务端）

2、OP 怎么发，不可能每次把全部的 value 发送到服务端？——刚开始假设全部发送到服务端

3、富文本以什么数据结构存储，DIFF 算法需要转换成树节点

4、冲突怎么处理？

对于在线协同文档，假设 A 和 B 在同时编辑同一个内容，我们处理冲突的方式有：

4.1 加锁。用户 A 在编辑时，就锁住文档，只能 A 进行更新。用户 B 就不能编辑，或编辑后提交修改被服务器丢弃；加锁体验太差，一个人在编辑时其他人就要干等着。

4.2 覆盖。谁最后修改，就全量使用他的修改，更早一些的其他人的修改会被丢弃。 覆盖则是导致用户的修改来回彼此覆盖，辛苦编辑的内容突然被别人覆盖掉了心情低落。

4.3 用户自行处理冲突。就像 git merge 导致的冲突一样，会提示哪个地方被同时修改了，让合并者手动选择使用哪一个修改；自行处理冲突则需要额外的操作步骤和成本，实时性很差，不适合高频同时修改的场景。

4.4使用一致性算法。比如我们要介绍的 OT 算法，可以让用户编辑进行算法处理进行调整，在多个客户端生成一致的修改结果。一致性算法是最好的选择，对用户最友好，不过带来了实现的复杂。

服务器端有冲突时，可以加个锁（例如腾讯文档中的表格，某个用户编辑某个单元格，那么其他人不能编辑，这样就避免冲突）如果多人协同，某个 OP 因为冲突没有合并到主分支，那么可以返回这个用户，由于冲突，当前结果未保存，建议刷新界面。

协同编辑主要的算法是 OT，简介如下：

OT 算法全名叫 Operation Transformation，你看从名字就对应了上面我说的转变算法。

假如我们把 A 提交的行为叫做 A，B 提交的行为叫做 B，现在后台就是一个简单的转发功能，告诉 A 的是 B，告诉 B 的是 A，然后就出现问题了

正确：所以后台是把每个人提交的行为转变一下再告诉别人，其实这个技术就是 OT 算法（在第三个节点还是第三个节点插入新的节点）。

也就是说你输入两个先后执行的行为，它会告诉你两个转换过后的行为，然后把 A'行为告诉 B，把 B'行为告诉 A，这样大家再应用就相安无事了。

参考腾讯前端团队的文档：转载自AlloyTeam：http://www.alloyteam.com/2019/07/13659/，原文如下：

相信大家或多或少都有使用过在线文档，国内的像我们在做的腾讯文档还有其他家的很多类似产品。今天主要为大家揭开在线协作的神秘面纱，那就是 OT 算法。

1 背景¶

在线文档，抽象一下，这些产品的模式都是富文本编辑器+后台，富文本编辑器产生内容，展示内容，然后后台负责保存。富文本编辑器现在业界已经有很多成熟的产品，像 codeMirror，这一块本身也是很复杂的一块，也不是咱们这次关注的重点方向。不知道大家平常在用这些产品的时候有没有思考过一个问题，在线文档编辑的时候产生冲突怎么办？

2 举个栗子¶

举个很简单的例子，现在大家的文本都是 ‘aaab’，A 用户在第 3 个字符行后面插入了一个 ‘c’，B 用户在第 3 个字符行后面插入了一个 ‘d’，这个时候 A 这边看到的是 ‘aaacb’，B 这边看到的是 ‘aaadb’, 我们假设 A 用户先提交了数据，那其实最后预期的数据其实应该是 ‘aaacdb’，这样就最大的保存了每个人的输入。那我们现在来看看正常情况下这里会发生什么： A 用户：

A 本地已经是 ‘aaacb’ 了，过一会儿，后台告诉它 B 也编辑了，编辑的行为就是**第 3 个字符行后面插入了一个 ‘d’**，那 A 这边执行了这个行为，最终变成了 ‘aaadcb’

B 用户：

B 本地已经是 ‘aaadb’ 了，过一会儿，后台告诉它 A 也编辑了，编辑的行为就是**第 3 个字符行后面插入了一个 ‘c’**，那 B 这边执行了这个行为，最终变成了 ‘aaacdb’

从上面的模拟过程可以看到，A 用户最后的结果其实是不正确的，但是 B 是正确的。

这里先解释一下大家可能会疑惑的地方：为什么 B 是过一会儿后台告诉它 A 编辑了，不是说 A 先提交了数据吗？其实这里针对的是冲突场景，这里如果 B 在提交之前，已经收到后台告诉它 A 编辑了，那其实就是顺序编辑了，也就不是冲突了。所以这里指的是 A，B 几乎同时提交，但是 A 到达后台还是快一点的，也就是 A，B 在编辑的时候是不知道彼此的存在的。

真实的冲突场景其实不是这种简单的时序问题，这里我后面再介绍。

3 尝试解决¶

这里可能有一些聪明的小伙伴有了一些想法。

解决方案一：丢了丢了¶

这可能是最简单粗暴的方法了，我发现有冲突，就告诉用户，主子，咱这里有冲突了，臣妾解决不了啊。但是显然这会经常出现，然后主子就把你打入冷宫了。

解决方案二：锁¶

有些小伙伴想到，上面出现问题，还不是因为大家编辑了都立即应用了，我们编辑后不立即应用不就好了，而且历史告诉我们，有冲突加锁应该可以解决。那我们看看假如不立即应用，咱有没有什么处理办法： A 用户：

A 本地已经是 ‘aaab’ 了，A 编辑了，但是不应用，先发后台

B 用户：

B 本地已经是 ‘aaab’ 了，B 编辑了，但是不应用，先发后台

后台：

后台先收到 A 请求，然后加了一个锁，然后收到了 B 请求，这时侯应该是加锁的状态，所以接受了 A，拒绝了 B

A 用户：

A 用户收到了后台的回复，告诉它你的提交我接收了

B 用户：

B 用户收到了后台的回复，告诉它你的提交被我拒绝了，因为冲突了

这样虽然能继续下去，但是好像还是不太行的亚子啊，B 的提交还是丢了，所以好像和第一种简单粗暴的方法没啥区别

4 OT 算法¶

顺其自然的，这个时候你会看到 OT 算法驾着七彩祥云来救你了～其实回到上面的例子，本质问题还是因为后台通知大家的 B 的编辑行为看起来不太对。现在后台通知大家的是:

B 的编辑的行为就是**第 3 个字符行后面插入了一个 ‘d’**

但是在 A 已经接受的情况下，正确的通知应该是：

B 的编辑的行为就是**第 4 个字符行后面插入了一个 ‘d’**

假如我们把 A 提交的行为叫做 A，B 提交的行为叫做 B，现在后台就是一个简单的转发功能，告诉 A 的是 B，告诉 B 的是 A，然后就出现问题了。所以后台应该更聪明一点，它应该学会一个招术，那就是把每个人提交的行为转变一下再告诉别人，其实这个技术就是 OT 算法。

OT 算法全名叫 Operation Transformation，你看从名字就对应了上面我说的转变算法。假设我们的 OT 算法的转换功能叫 transform，那 transform（A，B）= A',B'。也就是说你输入两个先后执行的行为，它会告诉你两个转换过后的行为，然后把 A'行为告诉 B，把 B'行为告诉 A，这样大家再应用就相安无事了。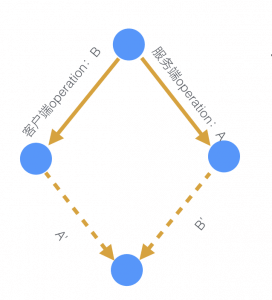上面的图是 OT 的经典菱形图，也就是说 A 会变成 A'在 B 这边执行，B 会变成 B'在 A 这边执行。这里实际抽象一下，用户永远就只有两个人，一个是自己，一个是服务端，只是服务端的操作可能来自很多人，如果不这样抽象，那一个个进行冲突处理可能会让你觉得无法理解。那我们现在再来看看后台有了 OT 这个能力之后会发生什么：

A 用户：

A 本地已经是 ‘aaacb’ 了，过一会儿，后台告诉它 B 也编辑了，编辑的行为就是**第 4 个字符行后面插入了一个 ‘d’**，那 A 这边执行了这个行为，最终变成了 ‘aaacdb’

B 用户：

B 本地已经是 ‘aaadb’ 了，过一会儿，后台告诉它 A 也编辑了，编辑的行为就是**第 3 个字符行后面插入了一个 ‘c’**，那 B 这边执行了这个行为，最终变成了 ‘aaacdb’

现在 A、B 就一致了！

5 OT 算法的实现¶

现在 OT 算法对我们来说就是一个黑盒，我们知道给一定的输入，它会有正确的输出，但是它是如何做到的呢？在介绍它的实现之前，我们需要抽象一下我们的操作行为，在之前我们的描述都是

第 3 个字符行后面插入了一个 ‘d’

这里怎么转换成程序识别或者能用代码表达的呢？其实这也是 OT 的关键。这里我直接揭晓答案：所有对文本的操作都可以抽象成三个原子行为：

R = Retain，保持操作 I = Insert，插入操作 D = Delete，删除操作

那之前的行为

第 3 个字符行后面插入了一个 ‘d’

就会变成

R(3), I('d')

也就是保持三个字符后插入 1 个 ‘d’，其实应该也很好理解，这里的操作就像操作数组一样，不管干什么，第一步你得先找到操作的下标。有了这三个原子以后，我们就可以看到：

A = R(3),I('c') B = R(3), I('d')

一切准备就绪，我们可以开始看 OT 了，这里 OT 算法现在已经很成熟了，这里我以一个 github 上的 repo 为例：ot.js 我们可以看看它的核心代码 (有删减，理解起来可能会比较复杂，感兴趣的可以深入思考一下)：

// Transform takes two operations A and B that happened concurrently and
// produces two operations A' and B' (in an array) such that
// `apply(apply(S, A), B') = apply(apply(S, B), A')`. This function is the heart of OT.
// 上面这个公式就是OT的核心，它产生了A',B',同时保证执行结果一致，S就是我们开始的状态，可以把这个和菱形图对应起来
// 整体执行流程有点像合并排序的过程。两个下标指针分别往前走

TextOperation.transform = function (operation1, operation2) {
  // operation1， operation2就是我们的A，B

  var operation1prime = new TextOperation(); // 就是A'
  var operation2prime = new TextOperation(); // 就是B'
  var ops1 = operation1.ops, ops2 = operation2.ops;
  var i1 = 0, i2 = 0;
  var op1 = ops1[i1++], op2 = ops2[i2++];
  while (true) {
    // At every iteration of the loop, the imaginary cursor that both
    // operation1 and operation2 have that operates on the input string must
    // have the same position in the input string.
    // 其实这里就是说transform的核心是保证两者的下标一致，这样操作的才是同一个位置的数据
    // ...
    // next two cases: one or both ops are insert ops
    // => insert the string in the corresponding prime operation, skip it in
    // the other one. If both op1 and op2 are insert ops, prefer op1.
    // 如果A是插入操作，A'一定也是插入，但是B'就不一样了，因为A是插入，不管你B是啥，你先等等，所以retain一下，保证下标一致
    // 这里实际上有三种情况，A是插入，B可能是R，I，D
    if (isInsert(op1)) {
      operation1prime.insert(op1);
      operation2prime.retain(op1.length);
      op1 = ops1[i1++];
      continue;
    }
    // 如果B也是插入，那B’就是插入，但是你的A'也得retain一下，保证下标一致
    // 这里可能有两者情况，A可能是R，D
    // 实例化思考一下，A [R(3),I('a')],B [I('b')],那对于A'来说就应该是[R(4),I('a')]
    if (isInsert(op2)) {
      operation1prime.retain(op2.length);
      operation2prime.insert(op2);
      op2 = ops2[i2++];
      continue;
    }
    // ...
    var minl;
    if (isRetain(op1) && isRetain(op2)) {
      // R和R处理
    } else if (isDelete(op1) && isDelete(op2)) {
      //D和D处理
    } else if (isDelete(op1) && isRetain(op2)) {
      // D和R处理
    } else if (isRetain(op1) && isDelete(op2)) {
      //R和D处理
    }
  }
  return [operation1prime, operation2prime];
};

这里就是 OT 的 transform 实现，本质上就是把用户的原子操作数组拿到以后，然后做 transform 操作，这里我只选了一小段来大概解析下，具体的可以看注释，其实原本的注释已经很全了。其实上面那段代码，因为我们的原子操作只有三种，根据排列组合，最多只会有 9 种情况，只是上面把很多情况合并了，你要是不理解，也可以拆开，帮助理解。其实上面的文件还有 compose，invert 等方法，但是其实 transform 才是我们理解的核心，其他方法大家感兴趣可以看看注释和下面贴的一些关于 OT 更详细介绍的文章。

6 OT 算法的时序¶

简单的 OT 大家只要理解了，好像也并不是很难，但是其实真实情况下 OT 会比想象的还要复杂，因为之前说的菱形会无限拓展。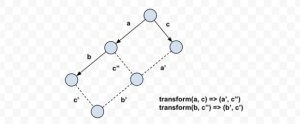简单理解一下，就是 A 本地产生了两次编辑，B 产生了一次。这里就必须要和大家解释一下之前遗留的时序问题了，不然可能无法理解。

之前说的时序都是指时间先后顺序，冲突也是指同时产生编辑。但是其实这里的同时不是时间上的同时，而是版本上的同时。也就是说我们需要用一个东西表示每一个版本，类似 git 的每次提交，每次提交到服务端的时候就要告诉后端，我的修改是基于哪个版本的修改。最简单的标志位就是递增的数字。那基于版本的冲突，可以简单理解为我们都是基于 100 版本的提交，那就是冲突了，也许我们并不是同时，谁先到后台决定了谁先被接受而已。这里最夸张的就是离线编辑，可能正常版本已经到了 1000 了，某个用户因为离线了，本地的版本一直停留在 100，提交上来的版本是基于 100 的。

那有了时序的概念，我们再看上面这个菱形，它可以理解成 A 和 B 都基于 100 提交了数据，但是在 A 的提交还没被后台确认的时候，A 又编辑了，但是因为上一次提交没被确认，所以这次不会发到后台，这时服务器告诉它 B 基于 100 做了提交。

这种情况下如何处理，就有点类似于 OT 落地到实践当中，你怎么实现了，上面提到的 github 的那个 repo 的实现其实非常巧妙，你看完注释应该就能全部理解，这里给出代码链接

精华就在于它把本地分成了几个状态：

Synchronized 没有正在提交并且等待回包的 operation AwaitingConfirm 有一个 operation 提交了但是等后台确认，本地没有编辑数据 AwaitingWithBuffer 有一个 operation 提交了但是等后台确认，本地有编辑数据

剩下的就是在这三种状态下，收到了本地和服务端的数据，分别应该怎么处理

结语¶

其实 OT 对应的只是一种思想，具体怎么实现是根据具体情况来区分的，比如我们现在讨论的就是文本的 OT，那有可能图的 OT、表格的 OT 又是其他的实现。OT 的核心就是 transform，而 transform 的核心就在于你怎么找到这样的原子操作了，然后原子操作的复杂度决定了 transform 实现的复杂度。

上面这个 repo 只是帮你实现了文本的协同处理，其实对于在线文档来说，还有样式的冲突处理，感兴趣的可以自己搜索相关资料了解一下，建议精读一下 ot.js 这个库。

最后如果读完这篇文章你对在线协作有了一定的认知，那这篇文章的使命也就达到了，最后如果有写的不正确的地方，欢迎斧正～

参考资料¶

另一个简单的小案例¶

从起始版本 T 开始，它接受了两个 并发操作 A 和 B。我们使用 trasform 方法生成 A’ 和 B’。我们有：

S + A + B' = T
S + B + A' = T

这样，从 S 得到相同的 T，保证了一致性。

const s = '12'; // 原始文案（版本 1）

// 在位置 3 插入 'A'
const oA = new TextOperation().retain(2).insert('A');

// 上述操作后得到结果 '12A'（版本 2）
const t1 = oA.apply(s);

// 收到 oB 操作：在位置 2 插入 'B'
const oB = new TextOperation().retain(2).insert('B');

// transform 拿到修正后的 [oA', oB'] 这是核心算法
// 我们这里只需要 oB'，它被修正为在位置 3 插入 'B'
const [oAp, oBp] = TextOperation.transform(oA, oB);

// 应用 oB'，结果为：12AB （版本 3）
const t2 = oBp.apply(t1);

// 另一个人执行 oAp 得到相同的 T 结果，协同算法满足结果

当然，如果数据结构是树，图等复杂的操作，不同原子操作需要不同的 transform 函数实现，以及考虑时序多个 ops 的合并。

Last update: November 9, 2024