你靠哪些讲解学会了曾经怎么也学不会的算法？¶
统计信息：字数 42077 阅读85分钟
====分割线====
1.快速排序（noip2016初赛）
2.后缀数组（2009国家集训队论文）
3.FFT （某个福建省的课件，内容为miskcoo的blog）
4.生成函数（某个名为polynomial的课件）
5.KD-Tree（2018.1 yali集训）
还有很多。
我认为大部分算法（数据结构），都是彻底理解后，不看板子能独立实现，才能真正学会。如果只是靠背的话，不会做题不说，过不了几天就会忘得一干二净。
比如 后缀自动机 我至今无法理解这个奇怪的东西。因为没有好的讲解资料（clj的感觉讲的不怎么样，至少我看不懂），我已经前前后后背了3遍板子，到现在还只会用后缀数组写题。
毫不犹豫的答案：动态规划！¶
听到 动态规划 这个响亮的大名你可能已经望而却步，那是因为这个响亮的名字真的真的很具有迷惑性，不像递归、回溯和贪心等等算法一样，其文即其意，而动态规划则不同，很容易望文生义，真可谓害人不浅，今天我就带大家一起扒一扒 动态规划 的裤子。
第一点，大家在学习动态规划时**切忌望文生义，因为其名字与其思想八竿子打不着**。你可以自己起一个能让自己记住其思想的名字更好，比如递推公式法，状态转移方程法等等。
第二点，与其说动态规划是一个算法，还不如说是解决问题的方法论。
第三点，动态规划的一般形式就是求最优值，比如最长公共子序列、最大子段和、最优二叉搜索树等等。
废话不多说，进入正题！
原文作者：景禹 原文链接：动态规划之武林秘籍
动态规划的基本思想¶
动态规划算法与分治法类似，其基本思想就是将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合动态规划法求解的问题，经分解得到的子问题往往不是相互独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，以至于最后解决原问题需要耗费指数时间。然而，不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复结算了很多次。如果我们能够保存已经解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，从而得到多项式时间复杂度的算法。为了达到次目的，可以用一个表来记录所有已解决的子问题的答案，不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划的基本思想。
你看了肯定没有抓住重点，那就多读几遍，不过下面早已备好：
- 将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到原问题的解；
- 经分解得到的子问题往往不是相互独立的；
- 保存已经解决的子问题的答案，避免重复计算。
这就是要点，务必熟记于心，虽然将来我们会看到各种各样的例子都是印证。
动态规划的基本要素¶
动态规划算法就是将待求解问题分解成若干子问题，先求解子问题并保存子问题的答案避免重复计算，然后从这些子问题的解得到原问题的解。而如何断定一个问题是否可以用动态规划来解决，就需要掌握动态规划的两个基本要素，「最优子结构性质」 和**「重叠子问题性质」** 。
最优子结构性质¶
设计动态规划算法的第一步通常是要刻画最优解的结构。当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质 。问题的最优子结构性质提供了该问题可用动态规划求解的重要线索。
例如，最短路径问题有如下的最优子结构：
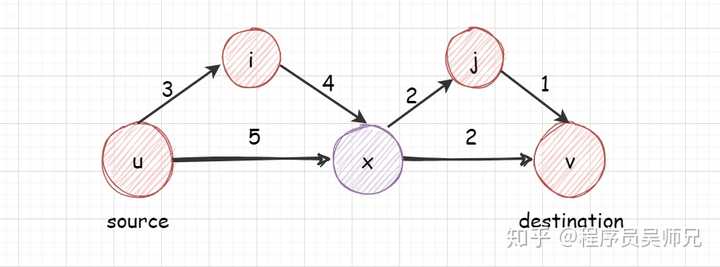
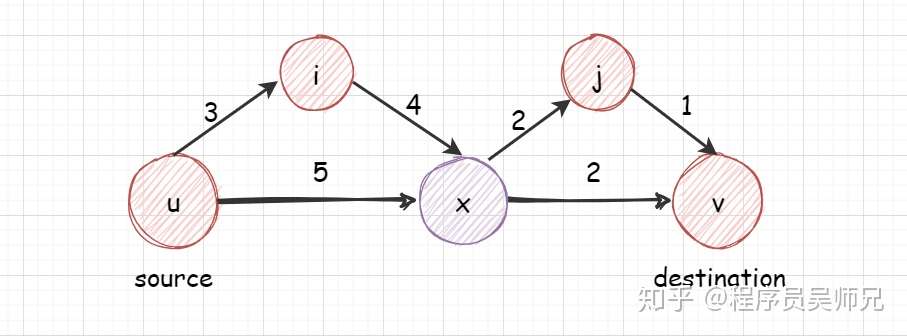
结点 x 是从源结点 u 到目标结点 v 的最短路径上的结点，则源结点 u 到目标结点 v 的最短路径 7 就等于从源结点 u 到结点 x 的最短路径 5 加上从结点 x 到目标结点 v 的最短路径 2 的和。源结点 u 到目标结点 v 的最短路径就是要求解的最优解，源结点 u 到结点 x 的最短路径和从结点 x 到目标结点 v 的最短路径均为子问题的最优解，而问题的最优解包含了其子问题的最优解，则该问题具有最优子结构性质。
弗洛伊德算法（ Floyd–Warshall Algorithm）和贝尔曼-福特算法（Bellman – Ford algorithm）都是解决单源点最短路径的经典动态规划算法，以后有机会定会给大家分享。
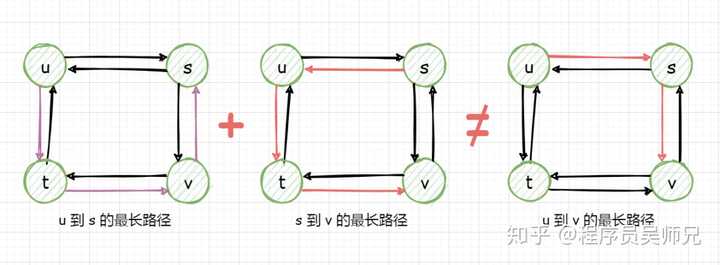
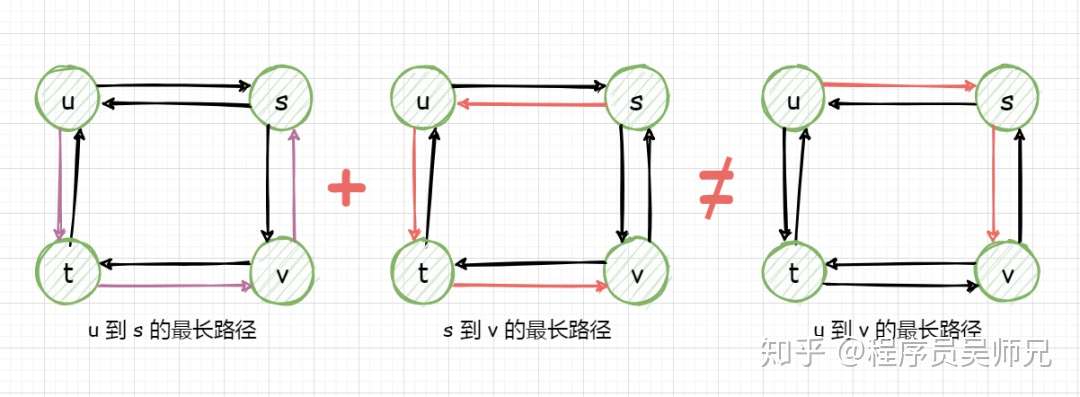
但是最长路径问题就不具有最优子结构性质，注意这里的最长路径指的是两个结点间的最长简单路径（即不存在环的路径）。盗用算法导论中的一张无权无向图就可以说明。
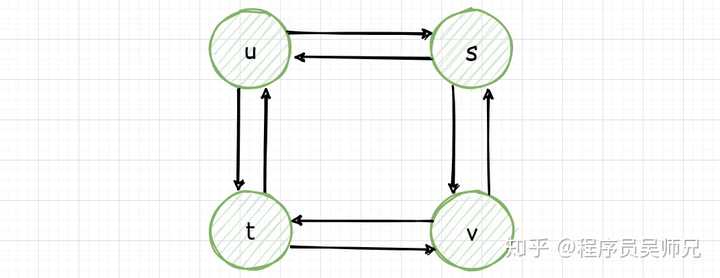
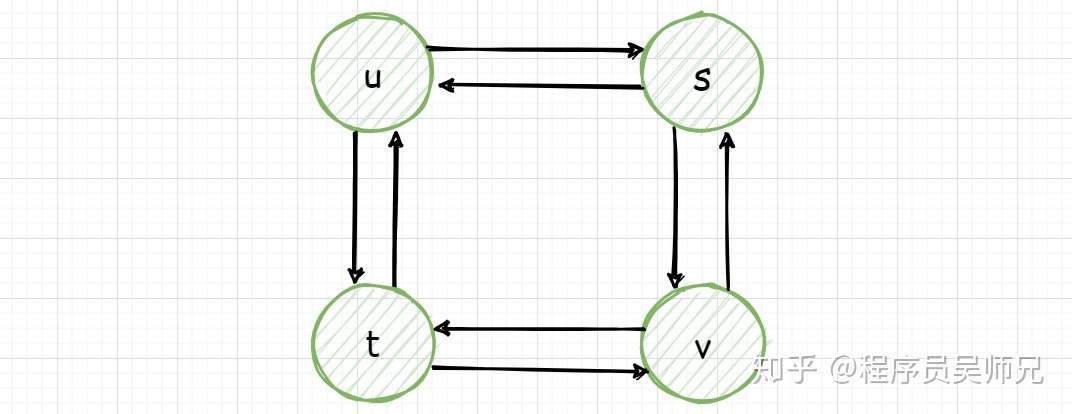
从结点 u 到结点 v 有两条最长路径，分别为 u → s → v 和 u → t → v ，但是与最短路径问题不同，这些最长路径不具有最优子结构性质。比如，从结点 u 到结点 v 有两条最长路径 u → s → v 并不等于从 u 到 s 的最长路径 u → t → v → s 与从 s 到 v 的最长路径 s → u → t → v 的加和。（更多最优子结构的例子，请持续关注景禹，笔芯）。
重叠子问题性质¶
在用递归算法自顶向下解决一个问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。动态规划正是利用了这种子问题的重叠性质，对每个子问题只解一次，而后将其解保存到一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。
光说不练假把式，重叠子问题谁不知道呀？
但还是要说一说，再练！！！
动态规划经分解得到的子问题往往不是相互独立的 。如果经分解得到的子问题的解之间相互独立，比如二分查找（Binary Search）经分解得到的子问题之间相互独立，不存在 重叠子问题，所以不适合用 动态规划，更适合分治算法。而斐波那契数列问题则更适用于动态规划，虽然严格意义上斐波那契数列的解决并不是动态规划的普适应用（动态规划的一般形式是求最优值！），但是对于我们理解动态规划的 「重叠子问题性质」 大有裨益！
关于斐波那契数列的递归实现，信手拈来：
int fib(int n)
{
if(n <= 1){
return n;
}
return fib(n-1) + fib(n-2);
}
虽然递归的代码简单易懂，但却极其低效。先不说这种递归实现造成栈空间的极大浪费，就仅仅该算法的时间复杂度已属于指数级别 了。
再来看看 n=5 时的递归树：
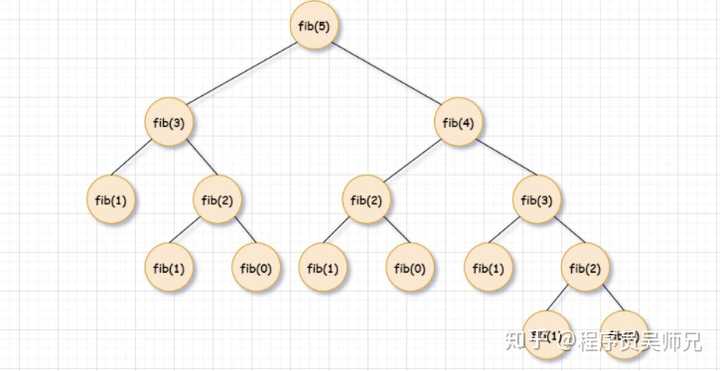
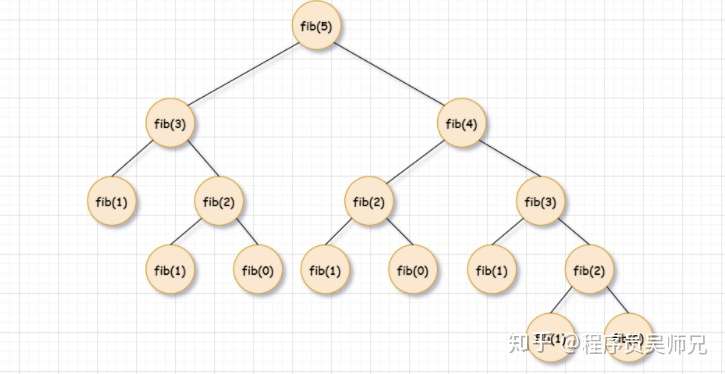
可以看到，fib(3) 被调用了两次，如果我们已经保存 fib(3) 的值，我们就可以复用保存的 fib(3) 的值，而不是重新计算，fib(2) 也是同样的道理。
保存重叠子问题的解（也就是 fib(3)）有以下两种方式：
DP table（自底向上）¶
DP table 就是动态规划算法自底向上建立的一个表格，用于保存每一个子问题的解，并返回表中的最后一个解。比如斐波那契数，我们先计算 fib(0)，然后 fib(1)，然后 fib(2)，然后 fib(3)，以此类推，直至计算出 fib(n)。
比如我们计算 fib(5)，先由 fib(0) + fib(1) 得到 fib(2)，再由 fib(1) + fib(2) 得到 fib(3)，再由 fib(2) + fib(3) 得到 fib(4)，最后由 fib(3) + fib(4) 得到 fib(5)。
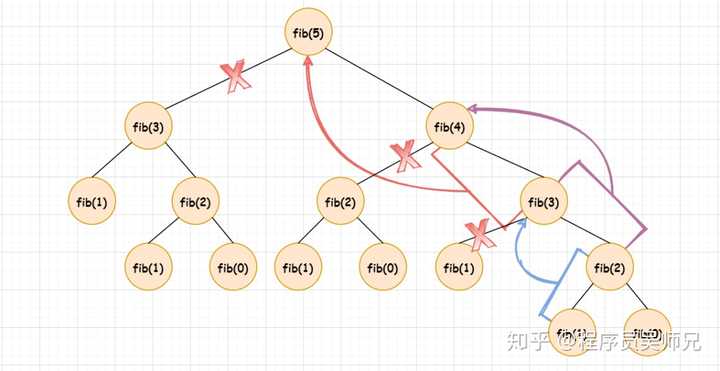
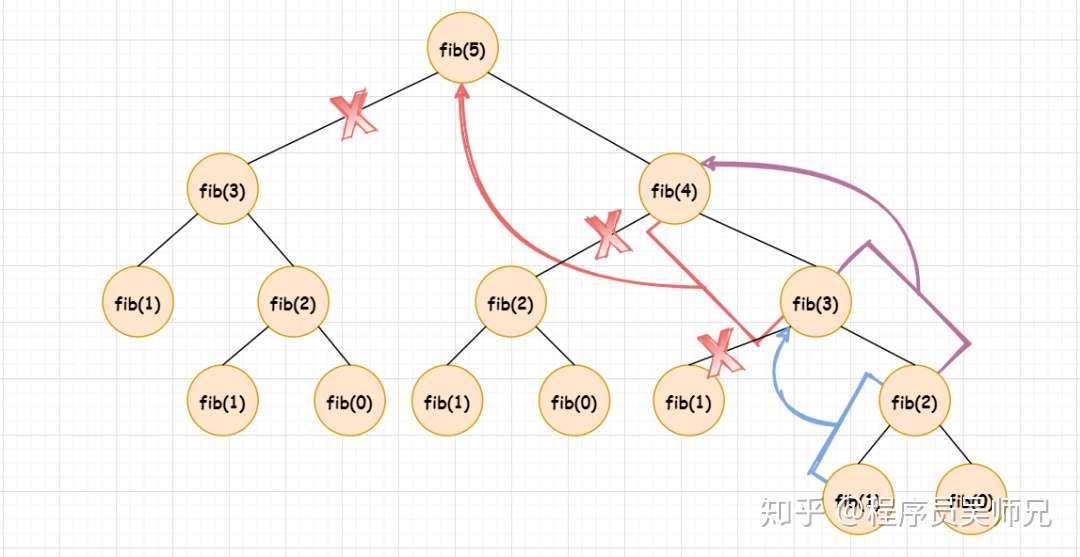
也就是说，我们只需要存储子问题的解，而不需要重复计算子问题的解，对上图进行简化：
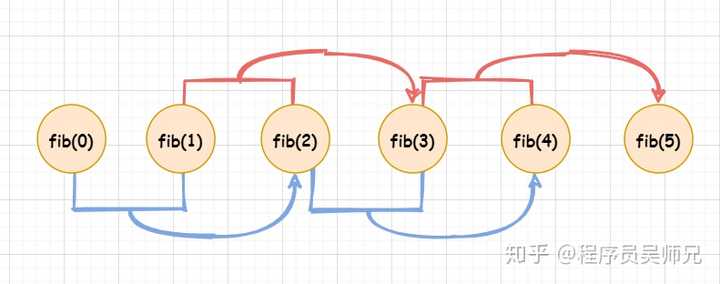
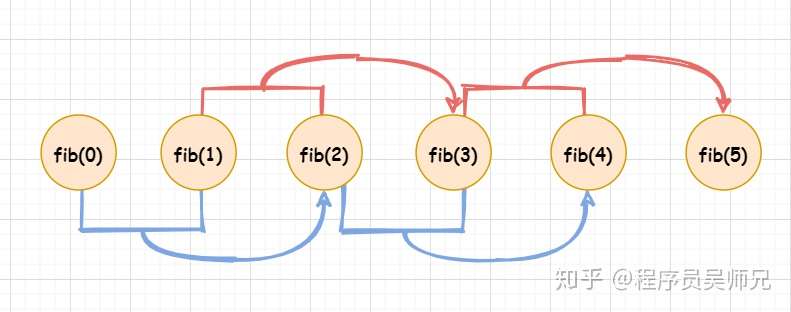
此图也就是动态规划法求斐波那契数的过程图。其实就实现而言，其实质上是斐波那契数的迭代实现，所以我之前说斐波那契数严格意义上不是动态规划所解决的问题，但是其对于我们理解**「重叠子问题性质」**还有很有帮助的。
对斐波那契数列问题，动态规划法（自底而上）保存重叠子问题的解的更一般形式为：
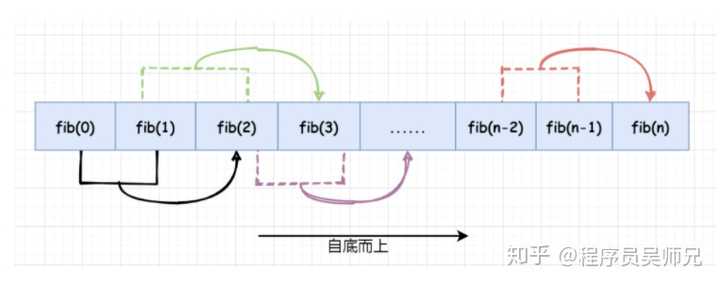
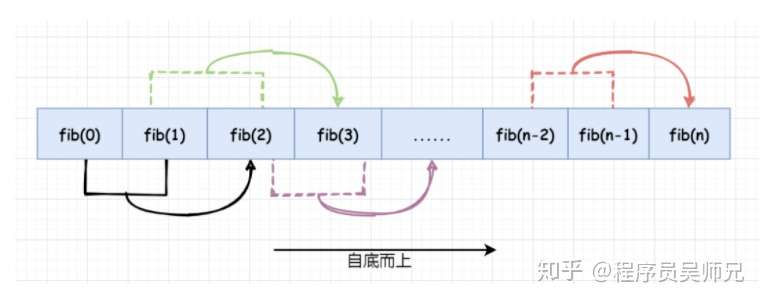
实现起来更是 so easy !
public class Fibonacci
{
int fib(int n)
{
int f[] = new int[n+1]; //保存子问题的解
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++)
f[i] = f[i-1] + f[i-2];
return f[n];
}
}
请不要问我上面的代码空间复杂度明明可以用 就实现，为什么我要写成 。因为希望大家理解动态规划法的一个核心思想，保存子问题的解，DP table 会保存所有子问题的解 。你期望的可能是下面这样，那也 OK。
public class Fibonacci
{
int fib(int n)
{
int result = 0;
int fib0 = 0;
int fib1 = 1;
for (int i = 2; i <= n; i++){
result = fib0 + fib1;
fib0 = fib1;
fib1 = result;
}
return result;
}
}
备忘录方法（自顶向下）¶
备忘录方法是动态规划算法的变形。与动态规划方法一样，备忘录方法用表格保存已解决的子问题的答案，在下次需要解此子问题时，只要简单地查看该子问题的答案，而不必重新计算。
与动态规划方法不同的是，备忘录方法的递归方式是自顶向下的，而动态规划算法则是自底向上递归的。因此，备忘录方法的控制结构与直接递归方法的控制结构相同，区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看，避免相同子问题的重复求解。
备忘录方法为每一个子问题建立一个记录项，初始时，该记录项存入一个特殊的值，表示该子问题尚未被解决（比如下面斐波那契数的备忘录版本中将其设置为 -1）。在求解过程中，对每个待求解的子问题，首先查看其相应的记录项。若记录项中存储的是初始化时存入的特殊值，则表示该子问题是第一次遇到，此时计算出该子问题的解，并保存在相应的记录项中，以备以后查看。若记录项中存储的已不是初始化时存入的特殊值，则表示该子问题已被计算过，其相应的记录项存储的是该子问题的答案。此时，只要从记录项中取出该子问题的答案即可，而不必重新计算。
以求解 fib(5) 为例，为求解 fib(5)，要先求解 fib(4)，要求解 fib(4)，要先求解 fib(3)，要求解 fib(2)，则要先求解 fib(1) 和 fib(0)，fib(1) = 1，fib(0) = 0，则直接返回，依次返回 fib(2) = 1，fib(3) = fib(2) + fib(1) = 2，fib(4) = fib(3) + fib(2) = 3，fib(5) = fib(4) + fib(3) = 5。
PS：递归调用可理解为入栈操作，而返回则为出栈操作。
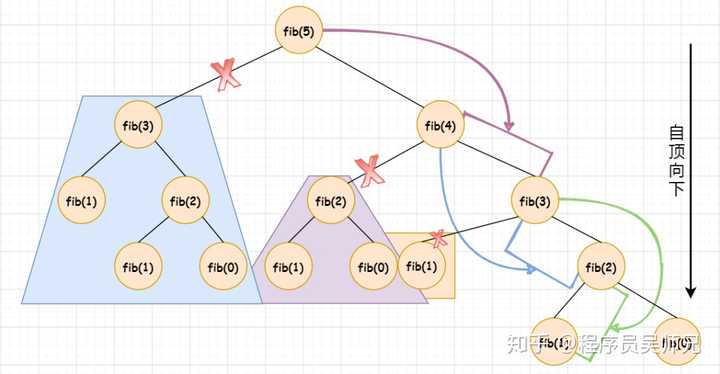
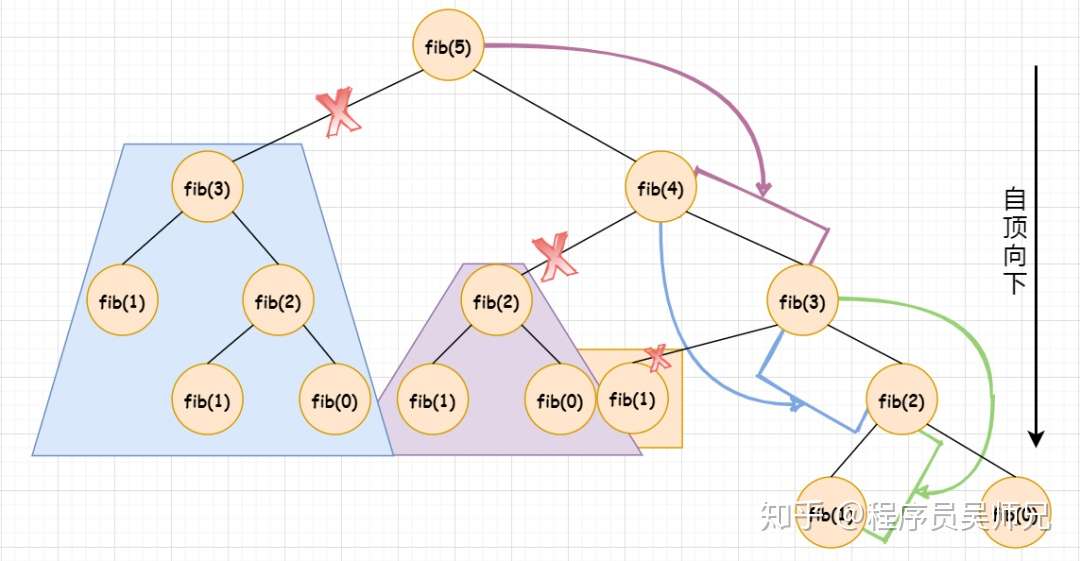
由 fib(5) 的递归树，可以发现，备忘录方法与动态规划方法一样，把一颗存在巨量冗余的递归树进行剪枝，改造成了一颗不存在冗余的递归图。重叠子问题的解都被保存了起来，用到时直接查表即可，而不需要重新计算，这一点备忘录与动态规划方法一样。不同的是，备忘录方法是自顶向下对问题求解，与直接递归方法的控制结构相同，而动态规划方法是自底向上对问题求解，与迭代实现方式的结构一致。
以 fib(5) 为例，备忘录方法（自顶向下）最终就是这样：
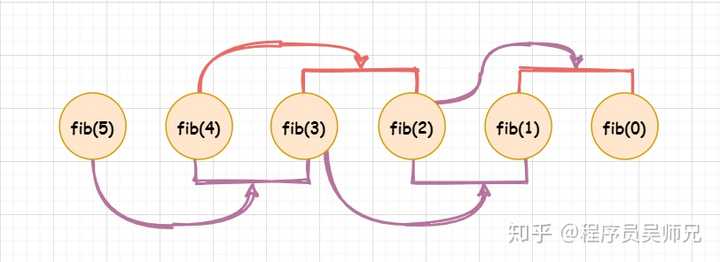
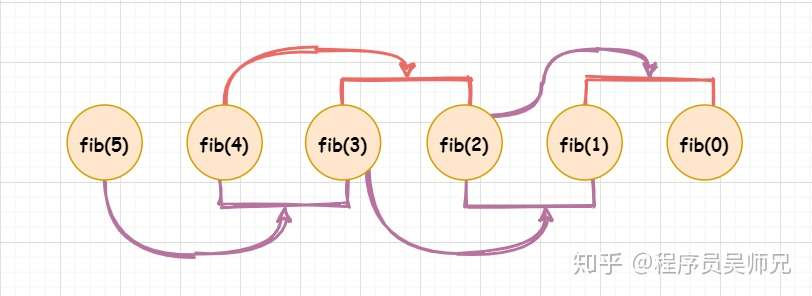
对任意一个斐波那契数，更一般的备忘录方法则为下图这样，与动态规划法正好相反：
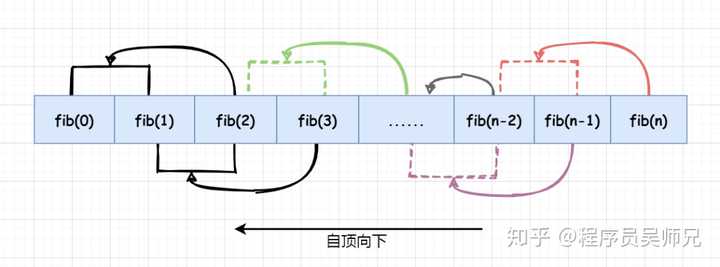
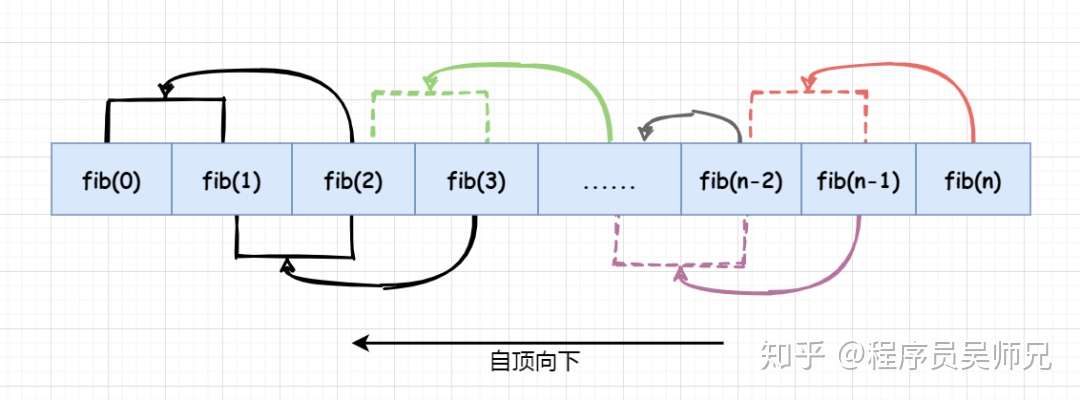
实现上只需要对递归实现进行稍加改动即可：
public class Fibonacci
{
final int MAX = 100; // 备忘录的大小
final int NIL = -1; // 特殊值
int lookup[] = new int[MAX]; // 备忘录数组
//初始化备忘录中的值为特殊值 NIL
void initializeTable()
{
for(int i = 0; i < MAX; i++)
{
lookup[i] = NIL;
}
}
//斐波那契数的备忘录版本
int fib(int n)
{
if(lookup[n] == NIL)
{
if(n <= 1)
{
lookup[n] = n;
}
else{
lookup[n] = fib(n-1) + fib(n-2);
}
}
return lookup[n];
}
}
动态规划方法（DP table）与备忘录方法都是存储子问题解的方法，除了解决问题的逻辑不同之外（一个自底向上，一个自顶向下），两者在时间效率上较为相近，关于两者的更多区别和相同点，以及如何选择文末解析。
上面讲的都是动态规划的一些基本概念，并不具有可操作性，下面带你真正扒一扒动态规划！
如何解决动态规划问题？¶
动态规划（**D**ynamic **P**rogramming，DP）是在多项式时间解决特定类型问题的一套方法论，且远远快于指数级别的蛮力法，而且动态规划的正确性是可以严格证明的。只不过这种证明对于解决动态规划问题并不具有决定性因素，所以此文也略去了。
解决动态规划问题四步法：
- 辨别是不是一个动态规划问题；
- 确定状态
- 建立状态之间的关系；
- 为状态添加备忘录或者DP Table 。
第一步：如何断定一个问题是动态规划问题？¶
一般情况下，需要求最优解的问题（最短路径问题，最长公共子序列，最大字段和等等，出现 最 字你就留意），在一定条件下对排列进行计数的计数问题（丑数问题）或某些概率问题都可以考虑用动态规划来解决。
所有的动态规划问题都满足重叠子问题性质，大多数经典的动态规划问题还满足最优子结构性质，当我们从一个给定的问题中发现了这些特性，就可以确定其可以用动态规划解决。
第二步：确定状态¶
DP 问题最重要的就是确定所有的状态和状态与状态之间的转移方程。确定状态转移方程是动态规划最难的部分，但也是最基础的，必须非常谨慎地选择状态，因为状态转移方程的确定取决于你对问题状态定义的选择。那么，状态到底是个什么鬼呢？
「状态」 可以视为一组可以唯一标识给定问题中某个子问题解的参数，这组参数应尽可能的小，以减少状态空间的大小。比如斐波那契数中，0 , 1, …, n 就可以视为参数，而通过这些参数定义出的 DP[0]，DP[1]，DP[2]，…，DP[n] 就是状态，而状态与状态之间的转移方程就是 DP(n) = DP(n-1) + DP(n-2) 。
再比如，经典的背包问题（Knapsack problem）中，状态通过 index 和 weight 两个参数来定义，即 DP[index][weight] 。DP[index][weight] 则表示当前从 0 到 index 的物品装入背包中可以获得的最大重量。因此，参数 index 和 weight 可以唯一确定背包问题的一个子问题的解。
所以，当确定给定的问题之后，首当其冲的就是确定问题的状态。动态规划算法就是将待求解问题分解成若干子问题，先求解子问题并保存子问题的答案避免重复计算，然后从这些子问题的解得到原问题的解。既然确定了一个一个的子问题的状态，接下来就是确定前一个状态到当前状态的转移关系式，也称状态转移方程。
第三步：构造状态转移方程¶
构造状态转移方程是 DP 问题最难的部分，需要足够敏锐的直觉和观察力，而这两者都是要通过**大量的练习**来获得。我们用一个简单的问题来理解这个步骤。
问题描述：给定 3 个数 {1，3，5}，请问使用这三个数，有多少种方式可以构造出一个给定的数 ‘n’.(允许重复和不同顺序)。 设 n = 6，使用 {1，3，5} 则共有 8 种方式可以构造出 ‘n’ ： 1+1+1+1+1+1 1+1+1+3 1+1+3+1 1+3+1+1 3+1+1+1 3+3 1+5 5+1
我们现在考虑用动态规划的方法论来解决。首先确定该问题的状态，由于参数 n 可以唯一标识任意一个子问题，我们用参数 n 来确定状态。所以，上述问题的状态就可以表示为 DP[n]，代表使用 {1，3，5} 作为元素可以形成 n 的总的序列数。
接下来就是计算 DP[n] 了，此时所谓的直觉就很关键了。
因为我们仅能使用 {1，3，5} 来形成给定的数字 n ，我们可以先考虑 n = 1,2,3,4,5,6 的结果，就是求出 n 等于 1，2，3，4，5，6 的状态值。
DP[n = 1] = 1，DP[n = 2] = 1, DP[n = 3] = 2，DP[n = 4] = 3，DP[n = 5] = 5，DP[n = 6] = 8。
现在，我们期望得到 DP[n = 7] 的值，我可以利用子状态的三种情况得到 n = 7 ：
一、给状态 DP[n = 6] 的序列均加 1，如下所示：
(1+1+1+1+1+1) + 1 (1+1+1+3) + 1 (1+1+3+1) + 1 (1+3+1+1) + 1 (3+1+1+1) + 1 (3+3) + 1 (1+5) + 1 (5+1) + 1
二、给状态 DP[4] 的序列均加 3
(1+1+1+1) + 3 (1+3) + 3 (3 + 1) + 3
三、给状态 DP[2] 的序列均加 5
(1 + 1) + 5
仔细检查并确认上述三种情况覆盖了所有可能形成和为 7 的序列，我们就可以说
DP[7] = DP[6] + DP[4] + DP[2] 或者 DP[7] = DP[7 – 1] + DP[7 – 3] + DP[7-5]
推广一下：DP[n] = DP[n – 1] + DP[n – 3] + DP[n-5]
此时我们就可以写出这样的代码了:
int solve(int n)
{
if(n < 0){
return 0;
}
if(n == 1 || n == 0){
return 1;
}
return solve(n-1) + solve(n-3) + solve(n-5);
}
但是这个递归解法的时间复杂度是指数级别的，因为递归解法重复计算了子问题的解。所以，第四步考虑加入备忘录或者DP Table 。
第四步：为状态添加备忘录或者 DP Table¶
这个可以说是动态规划最简单的部分，我们仅需要存储子状态的解，以便下次使用子状态时直接查表从内存中获得。
添加备忘录的代码：
public class DPSolution{
final int MAX = 100; // 备忘录的大小
final int NIL = -1; // 特殊值
int lookup[] = new int[MAX]; // 备忘录数组
//初始化备忘录中的值为特殊值 NIL
void initialize()
{
for(int i = 0; i < MAX; i++)
{
lookup[i] = NIL;
}
}
//备忘录版本
int solve(int n)
{
if(n < 0)
{
return 0;
}
if(n == 1 || n == 0){
return 1;
}
if(lookup[n] != NIL){
return lookup[n];
}
return lookup[n] = solve(n-1) + solve(n-3) + solve(n-5);
}
public static void main(String args[]){
DPSolution dp = new DPSolution();
dp.initialize();
System.out.println(dp.solve(20));
}
}
添加 DP Table 的代码：
final int MAX = 100; // 备忘录的大小
int solve(int n){
int DP[] = new int[MAX];
DP[1] = 1;
DP[2] = 1;
DP[3] = 2;
DP[4] = 3;
DP[5] = 5;
for(int i = 6; i <= n; i++){
DP[i] = DP[i - 1] + DP[i - 3] + DP[i - 5];
}
return DP[n];
}
备忘录 vs DP Table¶
被复用的子问题的解既可以使用备忘录进行存储，也可以使用 DP Table，那么到底哪种方法更好，两种方法应该如何抉择呢？带着问号画句号。
虽然在最开始介绍备忘录方法时已有涉及，但这里的讲解会更通俗。我们一起来看两个同学学习动态规划的方式。
同学一：为了掌握动态规划的内容，我首先会学习一些动态规划的理论，然后再考虑去用大量的动态规划问题进行练习。
同学二：为了掌握动态规划的内容，我必须练习一些经典的动态规划问题，为此我不得不学习一些动态规划的理论。
两位同学说的是同一件事情，区别在于两者传递信息的方式不同，同学一可以视为一种自底向上的方式，而同学二是一种自顶向下的方式。
DP Table 就是同学一所说的自底向上的方式，备忘录则是同学二所说的自顶向下的方式。
DP Table 法（自底向上的动态规划）¶
顾名思义，自底向上就是从底部（递归的出口，动态规划中称为 base case）开始，不断向上回溯，计算出问题的解。下面看一下 DP Table 的状态转移过程。
设 DP 问题的基态（Base State）为 dp[0] ，目标状态为 dp[n] 。
如果我们从基态 dp[0] 开始转移，在遵循状态转移方程的情况下到达目标状态 dp[n] ，则将其称为 “自底向上” 的方法。（dp[0] → dp[n]）
我们可以使用自底向上的方法计算一个数的阶乘。
定义状态：dp[x] 表示一个状态，即 x 的阶乘。
状态转移方程：dp[x] = dp[x - 1] * x .
int dp[] = new int[MAX];
int dp[0] = 1; // base state
for(int i = 1; i <= n; i++)
{
dp[i] = dp[i-1] * i;
}
上面的从基态 dp[0] 开始，经状态转移方程到达目标状态 dp[n] .
PS：注意这里的DP Table 是按照顺序填充的，并且我们直接从表中访问计算的子状态的解。
备忘录法（自顶向下的方法）¶
还是按照状态转移描述，我们从状态 dp[n] 开始，经状态转移向下寻找所需要的子状态的值，直到找到所有与状态 dp[n] 相关的子状态，并返回 dp[n] ，这就是自顶向下的备忘录方法。
我们用备忘录方法解决阶乘问题。
int dp[] = new int[MAX];
for(int i = 0; i < MAX; i++){
dp[i] = -1;
}
int solve(int x){
if(x == 0){
return 1;
}
if(dp[x] != -1){
return dp[x];
}
return (dp[x] = x * solve(x-1));
}
对于阶乘问题，内存布局是线性的，所以 dp[] 表是按照线性进行填充的。但是当考虑二维数组的情况下，就像最小成本路径问题一样，此时的内存将不是按照顺序存储。
状态：DP Table 状态转移关系较难确定，备忘录状态转移关系较易确定。你可以理解为自顶向下推导较为容易，自底向上推导较难。比如 DP[n] = DP[n – 1] + DP[n – 3] + DP[n-5] 的确定。
代码：当约束条件较多的情况下，DP Table 较为复杂；备忘录代码相对容易实现和简单，仅需对递归代码进行改造。
效率：动态规划（DP Table）较快，我们可以直接从表中获取子状态的解；备忘录由于大量的递归调用和返回状态操作，速度较慢。
子问题的解：当所有的子问题的解都至少要被解一遍，自底向上的动态规划算法通常比自顶向下的备忘录方法快常数量级；当求解的问题的子问题空间中的部分子问题不需要计算，仅需求解部分子问题就可以解决原问题，此时备忘录方法要优于动态规划，因为备忘录自顶向下仅存储与原问题求解相关的子问题的解。
表空间：DP Table 依次填充所有子状态的解；而备忘录不必填充所有子问题的解，而是按需填充。
至于两个该如何选择，我想你的心中也有数了，建议按照解动态规划的四步骤依次求解，至于第四步，你个人喜欢用 DP Table 就用 DP Table ，喜欢备忘录就用备忘录。
总结¶
可操作性的动态规划解题步骤：
第一步：断定一个问题是不是动态规划问题？（重叠子问题、最优子结构，“最” 字要注意）。
第二步：确定状态及其含义；
第三步：构造状态转移方程（根据题目给定的条件，枚举若干子状态，然后尝试用这些子状态构造出未知状态的解，就可以轻松得到状态转移方程，当然这一步离不开大量的练习）。
第四步：为状态添加备忘录或者 DP Table（根据个人喜欢，两者没有绝对的好坏之分）。
熟练掌握这四步套路，看它动态规划能玩出什么花样？
补充¶
在 LeetCode 里面有大量的和动态规划有关的题目，感兴趣的可以去做一下，看看自己有没有掌握动态规划。
然后顺便推荐一个阿里朋友的算法刷题的开源项目。
截至 2020 年 11 月，该开源项目配套的网站已经有一百二十万的访问量，在 GitHub 上收获了 8500 颗小星星。
这个开源项目是**@halfrost**（中文名**一缕殇流化隐半边冰**，简称**霜神**）去年刷算法题时整理出的 520 题，每道题都写了解题思路，全部都是 GO 实现的，并且每题都 runtime beats 100% 了。
至于为什么要求**每题都 runtime beats 100%**。
霜神是这样回复的：优化到 beats 100% 才算是把这题做出感觉了。有好几道 Hard 题，可以用暴力解法 AC 了，但只 beats 了 5%，这题就如同没做一样；而且面试中如果给了这样的答案，面试官也不会满意，“还有没有更优解？”。如果通过自己的思考能给出更优解，面试官会更满意一些。
如果你把这些题解都摸透，相信在面试环节你可以从容的回答“还有没有更优解”。
作者介绍：霜神是前阿里巴巴资深后端工程师，业余时间酷爱写博客，目前他的博客已经有 300W+ 的浏览量，是 iOS 开发届的大佬级别人物，霜神为人谦和，上周六我说能不能提供一份离线电子书，方便读者阅读，他立马熬夜研究，修改了好几个版本。
离线版笔记下载地址（已获授权）链接:https://pan.baidu.com/s/1aDa6_DVpwitWT4_F9x9XEA 密码: qif9
离线版笔记下载地址（已获授权）: LeetCode - Go 电子书下载
作者：九章算法 链接：https://www.zhihu.com/question/265531567/answer/1449818520 来源：知乎 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
必须是万恶之源的**动态规划**啊！每次刷到DP题，感觉上应该是要用动态规划解法，但总是没有思路，然后暴力解之。AC之后一看答案，原来是这样，我怎么就没想到……给人的感觉就是看完答案我都懂，下次遇到还是不会。
更难的是动态规划类型太多了，什么坐标型、序列型、划分型、背包型……甚至一道题可以用多种类型的DP解法。想要熟练掌握，刷题量就远比其他算法要多。最让人头秃的是有时候看到一道题，压根就不知道可以用DP来做，这就很难受了。后来一位清华学霸教了我一套**动态规划4步解题法，从此打开了新世界的大门。1.确定状态
2.转移方程
3.初始条件和边界情况
4.计算顺序我用一道经典题来说明下什么是4步解题法。你有三种硬币，分别面值2元，5元和7元，每种硬币都有足够多。买一本书需要27元。如何用最少的硬币组合正好付清，不需要对方找钱？原题练习：LintCode 669.换硬币关键词“用最少的硬币组合”——求最值问题，可以用动态规划来解决。顺便说下**可以使用动态规划的问题一般都有以下提问方式：****求最大值/最小值（从左上角到右上角路径的最大数字和、最长上升子序列长度）求方案数（有多少种方式走到右下角、有多少种方法选出K个数使得和是Sum）求存在性（取石子游戏，先手是否必胜；能不能选出K个数使得和是Sum）如果你碰到一个问题，是问你这三个问题之一的，那么有90%的概率是使用动态规划来求解。要重点说明的是，如果一个问题让你求出“所有的”方案和结果，则肯定不是使用动态规划。再说回这道题，4步解题法：****第一步，确定问题状态**状态在动态规划中的作用属于定海神针。解动态规划时需要开一个数组，这里的“状态”就是指数组的每个元素f[i]或f[i][j]代表什么。确定状态需要两个意识：最后一步和子问题**1.最后一步**这道题中，我们不知道最优策略是什么，但最优策略肯定是K枚硬币a1,a2……aK面值加起来是27。这里的“最后一步”就是存在最后一枚硬币aK。除去aK，前面的硬币面值和为27-aK。
这里有两个关键点：① 我们不关心前面的K-1枚硬币是怎么拼出27-aK的，我们也不知道aK和K，但是我们确定前面的硬币拼出了27-aK。② 因为是最优策略，所以拼出的27-ak硬币数一定要最少，否则就不是最优策略。**2.子问题**现在问题变成了：最少用多少枚硬币可以拼出27-aK。也就是将原问题（27）转化成了一个子问题，而且规模更小（27-aK）。这种与原问题内核一致，但是规模更小的问题，就叫子问题。为了简化定义，我们设状态f(X)=最少用多少枚硬币拼出X。所以问题就从求f(X)变成求f(X-aK)我们目前还不知道最后的硬币aK面额多少，但它的面额一定只可能是⅖/7之一。如果aK是2，f(27)应该是f(27-2) + 1 (加上最后这一枚面值2的硬币）如果aK是5，f(27)应该是f(27-5) + 1 (加上最后这一枚面值5的硬币）如果aK是7，f(27)应该是f(27-7) + 1 (加上最后这一枚面值7的硬币）除此以外，没有其他的可能了。因为要求最少的硬币数，所以问题的解就可以这样表示：f(27) = min{f(27-2)+1, f(27-5)+1, f(27-7)+1}**第二步：转移方程**设状态f[X]=最少用多少枚硬币拼出X对于任意X，f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}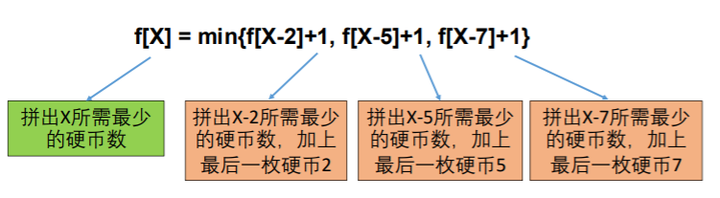
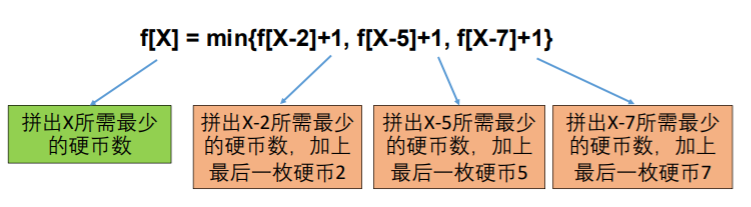实际面试中，如果正确列出转移方程，问题基本就解决一半了。很多同学基本也可以做到写出状态转移方程，但真正写程序的时候往往会出现很多错误或问题。 这就涉及到在写代码前的两个重要步骤，就是我们4步解题法的第三步和第四步。**第三步：初始条件和边界情况**f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}的边界情况是X-2, X-5或者X-7不能小于0（硬币面值为正）故对边界情况设定如下：如果硬币面值不能组合出Y，就定义f[Y]=正无穷例如f[-1]=f[-2]=…=正无穷；f[1] =min{f[-1]+1, f[-4]+1,f[-6]+1}=正无穷,表示拼不出1特殊情况：本题的F[0]对应的情况为F[-2]、F[-5]、F[-7]，按照上文的边界情况设定结果是正无穷。但是实际上F[0]的结果是存在的（即使用0个硬币的情况下），F[0]=0。这种用转移方程无法计算，但是又实际存在的情况，就必须通过手动定义。所以这里定义初始条件为：F[0]=0。而从0之后的数值是没矛盾的，比如F[1]= F[1-2]+1= F[-1]+1=正无穷（正无穷加任何数结果还是正无穷）；F[2]= F[2-2]+1= F[0]+1=1……**第四步，确定计算顺序**那么开始计算时，是从F[1]、F[2]开始？还是从F[27]、F[26]开始呢？判断计算顺序正确与否的原则是：当我们要计算F[X]（等式左边，如F[10]）的时候，等式右边（f[X-2], f[X-5], f[X-7]等）都是已经得到结果的状态，这个计算顺序就是OK的。实际就是从小到大的计算方式（偶有例外的情况我们后边再讲）。例如我们算到F[12]的时候，发现F[11]、F[10]、F[9]都已经算过了，这种算法就是对的；而开始算F[27]的时候，发现F[26]还没有算，这样的顺序就是错的。很显然这样的情况下写一个FOR循环就够了。回到这道题，采用动态规划的算法，每一步只尝试三种硬币，一共进行了27步。算法时间复杂度（即需要进行的步数）为27*3。 最后总结下**动态规划4步解题法**确定状态（研究最优策略的最后一步，转化为子问题）转移方程（根据子问题定义直接得到）初始条件和边界情况（细心，考虑周全）计算顺序（利用之前的计算结果）按照以上4步套路，基本上可以解决绝大多数类型的动态规划题。另外我在《国内大厂高频动规题详解**》分析了近3年国内大厂90%的高频动规笔面试题，可以帮你搞定7大动态规划题型，私信我【DP】可以享受9元听课优惠。
来来来，作为转码而且还没入门的码农，我来给大家示范一下我有多菜。因为本科不是CS的，和科班的人不一样，很多概念我根本没听过，自学起来也是难度满级。那咋办呢？那也只能硬着头皮学啊，看书，看视频，刷题呗。很多基本的概念是通过看了很多书和视频才学会的。给大家强调一下，基础，基础，还是基础是最重要的。把基础打牢，才能在后面的学习中厚积薄发。对于初学者来说更是如此，一开始别追求太难的东西，基础的东西学好了，再去学别的永远不迟。 递归。来个递归的定义吧。程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。[1] [2]递归三板斧：1.递归终止条件。什么时候停止递归，不需要计算，直接知道结果返回就行。2.递归调用自己，但传入一个更小的参数。3.怎么通过各种递归调用来组合解决当前问题。递归的例子有: 计算阶乘（n！），树的问题（Tree），二分法，快排，归并排序。把这些基础学好，其实能解不少一部分LeetCode的题呢。
[
来看看Google的暗黑笑话：
把亮点打到评论区吧。
其实递归的概念理解起来没那么难，但在编程里面用到复杂的问题下，那就难起来了。比如多叉递归，也就是回溯法，本质上还是利用递归去解题，只是每一层可以有多个选择。就会加一个for循环来写，加一个for循环，题目难道就一下子上去了。数独，N皇后的问题，还有背包问题的递归解，都是这一类。对于转码学算法的人，别提多难了，费老大的劲才能入门。而且理解了还得多练才能掌握。我一开始就遇到了不小的问题，看了不少课件和视频才慢慢有点感觉的。
其中CS61A的课，对Python的讲解还是很细致的。斯坦福的2018 Winter CS106B: Programming Abstractions对递归还有回溯的讲解让我慢慢对这些算法有了进一步的了解，尤其是教授把这些算法的执行过程画了出来，一点点去拆解神秘的递归过程。帮助还是蛮大的。红宝书配套的网站和教程的话，则真的是把常用的算法都讲得很透彻了，还配上高质量的Java源码，认真去学的人，肯定收获满满的。我就把这些对我特别有帮助的课程推荐给大家吧。网络课程的话，则是十二分强推UCB的CS61A。他们家的计算机系的CS61A，B，C课，简直制霸各种课程推荐列表。CS61A的官网在这里：https://inst.eecs.berkeley.edu/~cs61b/fa19/ 这门课以Python为主。2. 然后就是红宝书的网课以及配套官网：https://algs4.cs.princeton.edu/lectures/https://www.youtube.com/watch?v=1QZDe28peZk&list=PLRdD1c6QbAqJn0606RlOR6T3yUqFWKwmX3. 斯坦福2018 Winter CS106B: Programming Abstractions，虽然从名字不太能看出来，但其实是用C++讲数据结构，想用C++的小伙伴不容错过，我看了一半了，特别有帮助，尤其是对递归和回溯的讲解，简直醍醐灌顶。来一起学C++呀！如何啃下C++这块复杂又难学的硬骨头？已失效 现在因为不可知的原因，Youtube上面已经下架这门课程，但更方便的是，咱们可以在B站直接看：https://www.bilibili.com/video/av21620553?p=1www.bilibili.com4. MIT的算法课，教程用的算法导论，也是强推的网课：https://www.youtube.com/watch?v=HtSuA80QTyo&list=PLUl4u3cNGP61Oq3tWYp6V_F-5jb5L2iHb这门算法则基本不涉及到语言层面，主要是算法层面，讲得很好。
转码学习攻略总结：一个不是很了解CS（计算机科学）的人，该从哪里开始自学CS？www.zhihu.com
参考^https://baike.baidu.com/item/%E9%80%92%E5%BD%92^https://cs61a.org/disc/disc03_sol.pdf